Recursivitat

Una funció és recursiva si conté una crida a sí mateixa:

int recfun(int x) {
    //...
    int x = recfun(5); // <-- Crida recursiva
    // ...
}

La recursivitat és una forma alternativa d'escriure iteracions, i en molts casos dóna lloc a codi molt més simple. És important perquè en molts problemes (per exemple, els arbres a PRO2) la solució més raonable que podem escriure en poc temps és la recursiva.

Per a cada crida a una funció, es crea un nou context a la pila d'execució

Per poder entendre bé la recursivitat, cal primer entendre més a fons què passa quan cridem una funció:

int f(int x) {
    int res = x * 2 + 1;
    return res;
}

int main() {
    int n;
    cin >> n;
    cout << f(n) << endl;
}

La crida a la funció f des del main implica:

1. Que el main haurà de recordar "per on anava", és a dir, quina instrucció cal reprendre quan tornem de f amb el resultat (això s'ho apunta d'alguna manera).

2. Es crea un "context" per f, un espai propi a on f pot treballar, i a dins del qual hi ha totes les variables que f necessita (inclosos els paràmetres). En l'exemple, són x i res.

3. Abans de poder començar a executar f, cal copiar el valor de n del main a la variable x en el context de f.

4. Ara ja es pot executar f, que fa els seus càlculs i arriba a la instrucció return res amb el resultat de l'execució.

5. Es guarda el resultat de la crida a f momentàniament, però es destrueix el context de f (perquè ja no el necessitarem, ja que f ha acabat).

6. El main rep el resultat de f(n) i reprèn l'execució on era. El main estava esperant a poder mostrar per pantalla f(n) que és el resultat de cridar f.

En el moment en què f està acabant la seva execució, el diagrama que representa la situació és:

Cada caixa del diagrama és un context, i cada context té les seves variables, amb els valors en aquell moment. La pila d'execució és una "foto" de com està el programa en un cert instant.

La pila d'execució acumula els contextos de totes les funcions que estan esperant un resultat

Vegem un exemple amb més funcions:

char post_incr(char& ch, int d) {
    char res = ch;
    ch += d;
    return res;
}

string rep(char c, int n, int d) {
    string res = "";
    for (int i = 0; i < n; i++) {
        res += post_incr(c, d);
    }
    return res;
}

string funny_word(int x) {
    return rep('a', x, 1) + rep('z', x, -1);
}

int main() {
    int k;
    cin >> k;
    cout << funny_word(k) << endl;
}

En aquest cas, si fem una "foto" de la pila el primer cop que s'executa post_incr (suposant que k és 3), tindrem:

El main ha cridat a funny_word amb un 3 (el valor de k). I es queda esperant a veure quin valor retorna funny_word per poder-lo treure per pantalla. Alhora, funny_word ha cridat a rep, perquè necessita concatenar dos strings que venen de dues crides a rep per poder donar un resultat. rep està a la primera iteració del for afegint caràcters a la seva variable res, però per afegir el caràcter està esperant què valdrà la seva crida a post_incr.

Per tant, excepte post_incr, la resta funcions que apareixen a la pila d'execució estan a mig càlcul, esperant un valor que necessiten per continuar, i que la funció de sobre a la pila els ha de proporcionar.

En programes complexos, la pila d'execució, en certs moments, pot tenir una alçada de desenes i fins i tot centenars de funcions esperant.

Podem produir un "bucle infinit" amb una funció recursiva

Donat que una crida a una funció crea un nou context a la pila, si una funció es crida a sí mateixa i res més

void petit_mal() {
    petit_mal();
}

cada cop que la cridem crearà un context, i quan executem la funció en el nou context, en crearà un altre a sobre per a la nova crida, i així successivament.

Degut a que la pila d'execució sol tenir un tamany fixe (de 8 o 16MB, típicament) l'espai disponible per poder crear contextos és limitat, i tard o d'hora la funció petit_mal intenta crear un nou context i no hi ha espai per fer-ho, amb la qual cosa es produeix un "desbordament de pila" (o stack overflow), que aborta el programa de cop.

Per tant, mai es pot fer una funció recursiva que sempre s'executi a si mateixa. Hi ha d'haver algun cas en què la funció faci una altra cosa i per tant la cadena de crides recursives es trenqui.

El cas en què una funció recursiva no s'executa a sí mateixa es diu "cas base"

Canviem una mica la funció petit_mal per fer alguna cosa més útil:

void countdown(int n) {
    cout << n << endl;
    countdown(n - 1);
}

Si cridem countdown(100), es produirà un desbordament de pila però abans almenys haurem vist molts números per pantalla (100, 99, 98, 97, ...). Per curiositat, fins a quin número imprimeix la funció en el teu ordinador?? 😉

Per poder parar, necessitem un cas en què la funció no es cridi a sí mateixa, per tant, podem utilitzar el paràmetre n per fer-ho:

void countdown(int n) {
    if (n == 0) {
        return;
    }
    cout << n << endl;
    countdown(n - 1);
}

El cas base és el cas en què la funció no es crida a sí mateixa, i a countdown es dóna per a n igual a 0. En aquest cas (al que arribarem tard o d'hora si comencem amb un n positiu), la funció no fa res, perquè té un return just al començar. La instruccio return no retorna cap resultat, però marxa igualment de la funció, que és el que volem. I això fa que retorni de la crida i per tant la resta d'instruccions de la funció no s'executen.

Vegem més exemples del "cas base":

// rep_r('x', 3) --> "xxx"
// rep_r('$', 5) --> "$$$$$"
// rep_r('a', 7) --> "aaaaaaa"
// rep_r(' ', 0) --> " "
//
string rep_r(char c, int n) {
    if (n == 0) {
        return ""; // <-- cas base (0 repeticions)
    }
    return rep_r(c, n-1) + c;
}

// suma_digits(77) --> 14
// suma_digits(876) --> 21
// suma_digits(11111) --> 5
// suma_digits(0) --> 0
//
int suma_digits(int n) {
    if (n < 10) {
        return n; // <-- cas base (número amb un dígit)
    }
    return suma_digits(n / 10) + n % 10;
}

// suma una seqüència d'enters acabada en -1
int suma_sequencia() {
    int n;
    cin >> n;
    if (n == -1) {
        return 0; // <-- cas base (hem llegit el sentinella)
    }
    return n + suma_sequencia();
}

Comparem les dues solucions del problema "Comptant a's", a l'esquerra la iterativa i a la dreta la recursiva:

int count_as() {
    char c;
    int num_as = 0;
    cin >> c;
    while (c != '.') {
        if (c == 'a') {
            num_as++;
        }
        cin >> c;
    }
    return num_as;
}

int count_as() {
    char c;
    cin >> c;
    if (c == '.') {
        return 0;
    }
    int as = (c == 'a' ? 1 : 0);
    return as + count_as();
}

En una funció recursiva, la pila d'execució permet emmagatzemar els valors d'una seqüència

Tot i que el tema següent parla de vectors, que tenen com a funció principal emmagatzemar tots els elements d'una seqüència (quan això és necessari!), la recursivitat, implícitament, permet ja resoldre problemes que requeririen vectors, com ara mostrar una seqüència de paraules al revés:

void revessa() {
    string paraula;
    if (cin >> paraula) {
        revessa();
        cout << paraula << endl;
    }
}

Com hem explicat abans, cada cop que cridem revessa, es crearà un context i dins d'aquest hi haurà una variable paraula (una a cada context!). Quan la lectura té èxit, la paraula llegida per una crida a revessa queda en el seu context, i tot seguit es crea un nou context i la nova crida torna a llegir una paraula.

Amb la seqüència de paraules one two three four, la pila quedaria així:

Quan cridem la primera revessa, llegirà la primera paraula i cridarà la segona revessa, que llegirà la segona paraula, i així successivament. Per tant, s'anirà omplint la pila d'execució de contextos de revessa a on les variables paraula contenen els elements de la seqüència per ordre.

Un cop la lectura falla, la penúltima revessa està esperant, després de la crida recursiva, a poder imprimir la paraula, i per tant s'imprimeix four, i al retornar es reprèn el context del revessa de sota que mostrarà three, i la pila va baixant fins que no queden paraules i es torna al programa principal.

La única limitació de la versió recursiva amb respecte a la iterativa (que hauria de fer servir vectors) l'hem comentat abans, i és que la pila té un tamany limitat, i per tant, el tamany de la seqüència que ens hi cabrà és relativament petit (8MB a 16MB) amb respecte al que podriem emmagatzemar en un vector (tota la memòria, típicament 2GB o més).

Per escriure una funció recursiva, la podem programar suposant que ja disposem d'una versió correcta

El plantejament consisteix en fer el mínim de feina possible i "delegar" la resta en la crida recursiva (com si ens fes mandra d'acabar-ho), assumint que la funció és correcta. Aquesta suposició és el que s'anomena la hipòtesi d'inducció, i ens permet ignorar els detalls de la crida recursiva i centrar-nos en resoldre només la part més petita possible.

Per exemple, si ens demanen "comptar quants dígits d'un número són parells", podem pensar:

• Si no tenim dígits, el resultat és trivial (el cas base, que és 0).
• Obtenir el dígit de menys pes és senzill i determinar si és parell també.
• La resta de dígits els podem "delegar" a la mateixa funció recursivament (que treballi un altre!).

int digits_parells(int n) {
    if (n == 0) {
        return 0; // cas base: 0 dígits -> 0 dígits parells
    }
    int d = n % 10;
    int parell = d % 2 == 0;
    return (parell ? 1 : 0) + digits_parells(n / 10);
}

Es veu clar que digits_parells, en essència, processa un sol dígit. Només mira si és parell i afegeix 1 a la suma. Això és el que sembla màgia, perquè no hi ha cap iteració i sembla que quedi tota la feina per fer. Però el fet d'encadenar les crides entre sí fa que cada crida a la funció sigui com una volta d'un while o for, que fan poca cosa, però un cop s'han executat totes les iteracions, la feina està feta.

Per tant, fer funcions recursives és com muntar un circuit de fitxes de dòmino en filera, de tal manera que quan en fem caure una, caiguin totes les demés.

El debugger de VSCode permet observar la pila d'execució i les variables de tots els contextos de les funcions en espera

El debugger de VSCode (que es pot engegar amb F5), permet executar un programa pas a pas, i en particular, en el cas de funcions, permet entrar a una funció (F11) i executar-la pas a pas també (en comptes d'executar-la en un sol pas).

En el cas d'una funció recursiva, podem anar entrant en cada una de les crides amb F11 i si mirem el panell de l'esquerra, hi ha una secció anomenada "Call Stack", que mostra les funcions esperant a la pila d'execució:

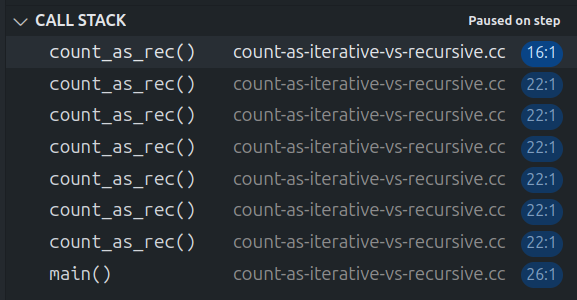
Clicant a cada funció podrem veure les seves variables i explorar tota la pila d'execució. Això permet entendre molt millor com s'organitzen les diferents crides a una funció recursiva.